LoRA in a nutshell
Large language models, like GPT-4, consist of billions of parameters, making them quite large and complex. This poses challenges for individuals and organizations who want to fine-tune these models to suit specific needs. The primary issues are the significant time required for training and the extensive GPU memory needed to handle such large models. Fortunately, a method known as LoRA (Low-Rank Adaptation) offers a solution for more efficient fine-tuning by reducing the number of parameters that need to be adjusted.
Precision in Model Storage
In most cases, the weights and activations within these models are stored in a 32-bit floating-point (float32) format. To estimate the size of a model, you can apply the following formula:
Model Size = Number of Parameters × Size of Each Parameter (in bytes)
This formula helps in understanding the memory requirements for storing and processing large language models, aiding in better planning and resource allocation for fine-tuning tasks.
The concept of reducing model size began to focus on the precision of data types. We found that using half precision, specifically float16, can maintain performance while reducing size. Another method is hybrid precision, where different parts of the neural network use different levels of precision.
FLOPS, or floating point operations per second, is a common measure of hardware speed.
To make this concept more intuitive, think of model precision like the resolution of a picture. Using lower resolution (half precision) can save space without significantly affecting the overall quality. Similarly, hybrid precision is like using higher resolution for important parts of the picture and lower resolution for less critical parts. This approach optimizes both performance and efficiency, ensuring that the model runs quickly without consuming unnecessary resources.
Fine-Tuning Techniques
Besides increasing computational speed by lowering precision or applying quantization, there has been research in Parameter Efficient Fine-Tuning techniques (PEFT). These methods allow fine-tuning large language models (LLMs) using fewer weights than the total number of weights. A few of these methods are:
- Transfer Learning:
The idea behind this is to freeze all weights and add a task-specific fine-tuning head. The downside is that we only get access to the output embeddings of the model and can’t learn based on its internal understanding and representation. - Adaptive Layers:
This approach involves adding new layers between the layers of a large model and then fine-tuning those. While generally effective, this method increases latency during inference and typically results in lower computational efficiency. - Prefix Tuning:
This is a lightweight alternative to fine-tuning, where we optimize the input vector for language models. By prepending specific input vectors to the model, we add context to steer the LLM. However, this method allows control of the model to a limited extent, which may not be sufficient in many cases. - LoRA (Low-Rank Adaptation):
This technique performs a rank decomposition on the updated weight matrices, making it a more efficient way to fine-tune models.
Making PEFT More Intuitive
Understanding the need for Parameter Efficient Fine-Tuning (PEFT) techniques is crucial in the context of working with large language models. Traditional fine-tuning involves adjusting all model weights, which can be computationally expensive and time-consuming, especially with very large models. PEFT techniques aim to reduce this burden by focusing on modifying a smaller subset of parameters or by using additional, lighter components that integrate with the existing model structure.
For instance, consider a scenario where a company wants to tailor a general-purpose language model for their specific customer service needs. Using PEFT, they can fine-tune the model efficiently without requiring extensive computational resources. Transfer Learning would allow them to add a task-specific head to handle customer queries, while Adaptive Layers could enhance the model’s understanding without overhauling its entire architecture. Prefix Tuning and LoRA provide lightweight alternatives that fine-tune the model in a more resource-efficient manner, making advanced language technologies accessible even to organizations with limited computational capabilities.
Low-Rank Adaptation (LoRA)
The rank of the a matrix tells us how many independent rows or column vectors exist in the matrix. Low rank means that the rank of the matrix is less than the dimensions of the matrix. Adaptation in the name is used to represent the fine-tuning process of the models.
LoRa is motivated by a paper published by Facebook research stating that there exists a low dimension re-parameterization that is as effective as the full parameter space. What this means is that certain downstream tasks do not need to tune all parmeters but instead can transform a small set of weight that can prove to be as effective. Based on this, LoRA paper was written by Microsoft Researchers, and they say that the change in model weights Δw also has a low intrinsic dimension. Formally this is done through rank decomposition:
W₀ are the weights of the large model and are untouched.
BA are both low rank matrices and their product is exactly the change in model weights Δw
Important note: We do not need to find the decomposition of Δw into B and A but rather we care about the other direction, that is we construct Δw by multiplying B and A. That also meant that they need to be initialised in such a way that Δw is 0 at the start of training. This is done by setting B to 0 and sampling the values of A from a normal distribution.
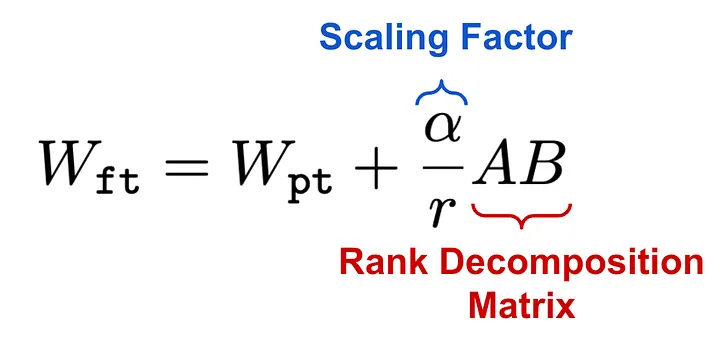
This decomposition can be applied on any dance neural network, but however in transformers it is generally applied on the attention weights. During the forward pass, the input is then multiplied by both, the original model weights and the rank decomposition matrices. Something as shown below:
Scaling Factor
In the paper, the knowledge of a pretrained rank in the denominator corresponds to the intrinsic dimension. This indicates the extent to which we want to decompose the matrices. Typical numbers range from 1 to 64 and express the amount of compression on the weights. The scaling factor, α, is used to control the influence of the decomposition on the original weights. It balances the knowledge of a pretrained model with the adaptation to the new task.
Both the rank, r, and alpha, α, are hyperparameters. If the ratio is 0, we get the original model. If it is 1, we get a fully decomposed model (LoRa model). The ratio can also be more than 1 if you want to emphasize the fine-tuning weights. The scaling helps to stabilize other model hyperparameters, such as the learning rate.
To put it simply, think of the scaling factor as a way to fine-tune how much of the original model’s knowledge we keep and how much we adapt it for new tasks. Imagine you have a piece of clay that represents your pretrained model. Decomposing the matrices is like molding this clay into a new shape for a different purpose. The rank determines how much you break down the clay, while alpha controls how much of the original clay shape you maintain versus how much you alter it. If alpha is 0, you keep the original shape entirely. If alpha is 1, you fully reshape it. Adjusting these factors allows you to balance between the original model’s performance and the new task’s requirements, ensuring stable performance during training.
Optimal Rank
In the LoRA (Low-Rank Adaptation) paper, various experiments demonstrate that very low ranks can already deliver impressive performance. Increasing the rank does not improve performance significantly because the data may have a small intrinsic rank. This, however, depends on the dataset.
When considering optimal rank, ask yourself whether the foundation model has seen similar data to your fine-tuning dataset. If your fine-tuning data is significantly different, a higher rank might be required.
Advantages of Using Low Ranks
- Fewer Weights to Tune: Lower ranks mean there are fewer parameters that need adjustment, simplifying the tuning process.
- Reduced Training Time: With fewer weights, the training process becomes faster, allowing for quicker model iterations.
- Lower RAM Usage: The reduced number of weights decreases memory requirements, making it more efficient to train models on machines with limited RAM.
- Easy Weight Integration: Weights from rank decomposition can be seamlessly merged into the original model by simply adding them.
- New Model Without Overhead: Unlike methods such as adapters, this approach allows you to create a new model without additional overhead.
Making It Intuitive
Imagine you are a chef fine-tuning a recipe. If your base recipe (foundation model) already includes similar ingredients (data), you don’t need to add much more (low rank). However, if your new recipe (fine-tuning data) is very different, you might need to add a lot of new ingredients (higher rank) to achieve the desired taste (performance). The key is to balance the amount of new ingredients while keeping the preparation (training) time and resources in check. This way, you can create a refined dish (model) efficiently, without overcomplicating the process.